从头开始的概率统计、信息论学习
写在最前面:本篇文章的基础来自B站UP主王木头学科学的视频,同时我会在其中补充一些其他资料,不断完善。
知识学习的两种模式
- 瀑布模式:教科书中采用的模式,比如在不学习到第三、第四章时不知道第一章学习的知识有什么用。在对学科还没有形成整体认识的时候,就会过早的掌握一些细枝末节,这反而会对整体的把握形成一个障碍。
- 迭代模式:先做一个总论,也就是先把知识细节的优先级调低,把最高的优先级放在对概率论、统计学和信息论互相之间的联系和整体的理解上。
本次学习采取的是迭代模式。
从概率论最基础的问题出发
概率论的核心议题:如何用数学的方式对不确定性或者说是对可能性这件事进行描述。
对于这个核心议题,该如何去解决呢?
下面会从建表的方法进行介绍,一步步完善,形成各个版本。
V1.0 版本

如图所示,通过一个表将事件及其可能性列举出来,同时为了简化可以为每一个事件带上编号。
由此,我们便可以得到一个数学形式的函数:f(S) =K,即输入事件返回该事件的可能性。
当然要想使用这个函数真的表示可能性还需要做一些限制:
- 数值K要满足可能性的相对关系,即若
事件A的可能性>事件B的可能性,则有数值1>数值2 - 数值要满足事件的包含关系,即若
事件c = {事件a,事件b},则有数值3 = 数值1+数值2
注意:这里的解决方案中对数值的大小没有限制,只要满足上面的条件即可,所以这里的数值表示的是可能性,而不是概率值。
通过观察我们可以发现这个方案是有问题的,它只是对可能性这件事进行了数学符号化,并没有解决数学化这个问题。
要想解决数学化这个问题,除了定义的体系能够自洽外,还要尽可能的简约,也就是奥卡姆剃刀原理即如非必要,勿增实体。上面定义的显然是不符合这个原理的,因为事件c的可能性是完全可以通过事件a和事件b推导出来的,没有必要单独去放到表中。换句话说,我们的表中只需要列举原子事件的可能性即可。
V2.0版本:引入原子事件

如图所示,只有不可再分的原子事件才需要被手动的赋予对应的数值。
由此就可以推导出更新后的函数定义:

这时候可能性即数值K就与概率值很像了。
但是这个函数定义还是有问题,因为我们可以得到这个函数是因为定义了原子事件,而原子事件本身便是有问题的。
- 对于离散事件可以很容易确定原子事件,比如掷骰子,可以将得到的点数作为原子事件;
- 但是对于连续事件呢,要使用区间去定义原子事件,这种情况下事件可以无限细分,这时如果再使用原子事件作为思考的起点,基于它建立描述可能性的数学体系,就可能会出现问题。
因为上述描述的原子事件的问题,我们很难再用左边表格作为地基去建立右边表格。
推不动就试一下拉,可不可以用右边的表格作为地基去建立数学体系呢?
V3.0版本:换用累计分布

先来看上面的两个表格,右边的表格是基础,其中域中的元素是事件;而左边表格里的S是样本空间,其中的元素不是事件。
定义中,上面的是累计分布函数,下面的是概论密度函数。
这里就是使用累计分布作为地基去建立概论学体系,可以将连续和离散两种情况统一起来。不同是下面定义的函数,对于离散情况其表示概率质量函数,对于连续情况表示概率密度函数。
至此,概论学的地基便打好了,接下来就算一层层扩展和封装,直到可以解决实际问题。
概率论的三层理解
- 最底层是概率空间和随机变量
这里要重点理解一下概论空间:(从数学的角度,而不是确定性去解释)
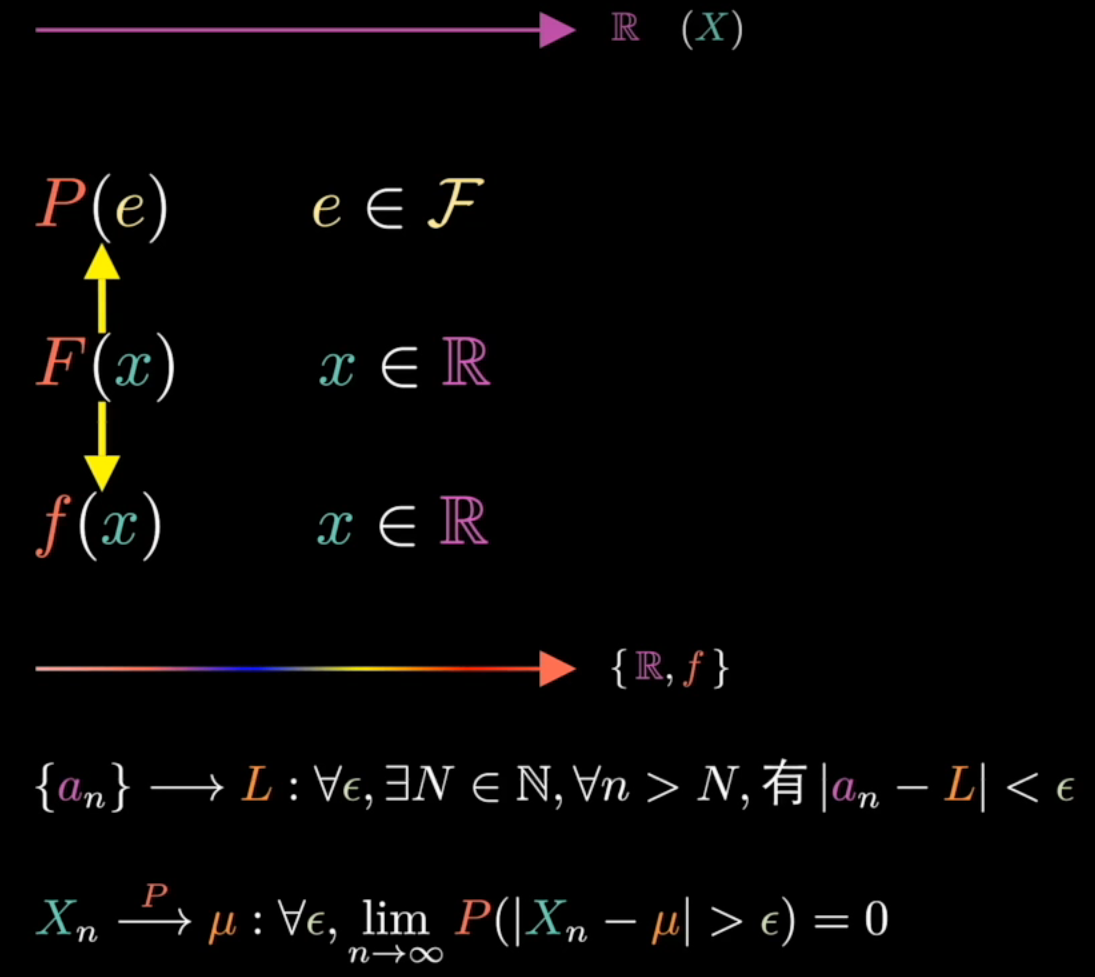
首先,任何一个样本空间都可以等价的对应到一个实数空间上去,就像上图中最上面的线。而P(e)表示的就是这个实数空间中一段或者几段的取值,也就是线段的长度。
之后,引入累计分布函数F对P进行重新定义,再进一步就可以得到密度函数f。这个密度到底是什么呢,其实就是给实数空间的每一个点赋予一个额外的描述。
所以对于概率空间就可以这样理解:具体的x的取值代表这个点在空间中的位置信息,而这个点对应的密度函数的取值则是这个点在整个实数空间的权重。
所以仅从数学角度上理解,概率空间就是一个被赋予了权重的实数空间,就像上图中最下面的线。
在纯实数中,两个点的距离就是二者的差值,而在概率空间中两个点的距离是二者对应权重的差值,即对距离这个概念进行了重新的定义。所以要想表示收敛,就是要权重趋于0才可以。
总结:
密度就是概率空间中一个点的权重值质量就是概率空间中一个或者多个线段的权重值
- 第二层是多维描述
即将原始的线升级到面、体等,为每一个面积、体积加上权重。
从这个概念上来看,从密度的角度理解概率比从累计分布角度上理解更加直观。

如上图,是一个二维空间里的密度函数,就相当于在二维的空间里定义了一个场,而每一个点的累计分布函数就是这个点的左下角所有面积的权重值。
这个描述二维空间的密度函数值的函数就叫联合概论密度函数。而边缘概率和条件概论就是两个降维考虑问题的方式。
先来看边缘概率密度:
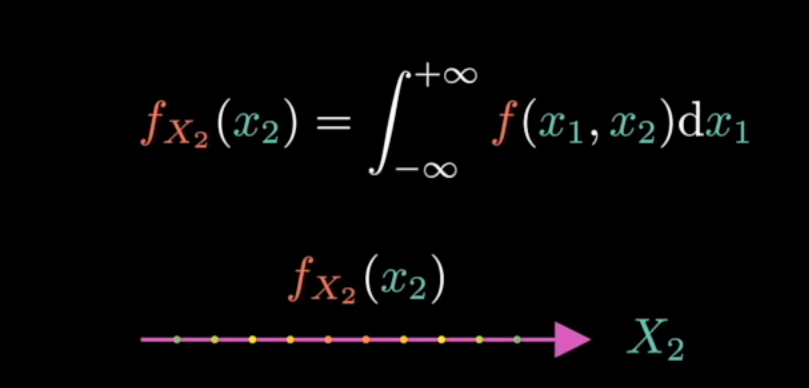
其获取概率密度的方式就是将原本的联合概率密度函数沿着某一个x轴进行压缩,或者说压扁了。
再看看条件概率:
先不用管公式,我们可以这样理解条件概率

- 在联合概率密度的图像取x2 = a的线,即为分子,但是这个线只是二维图的一部分,所以是不归一的。
- 之后通过分母将其等比例放大,使得这一条线的权重值归一,这个分母就是x2 = a这条线的总权重值。
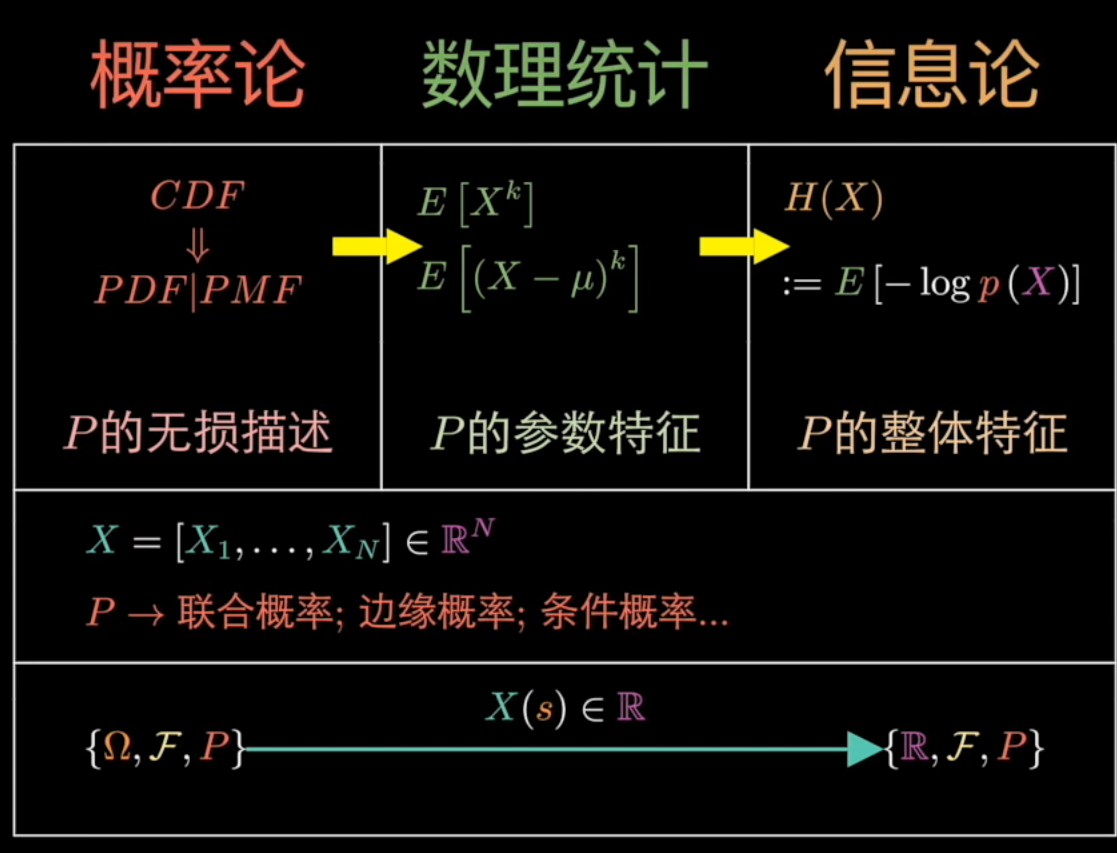
- P的三种不同描述
P的无损描述:就是前面介绍过的累积分布函数和由其推导得到的密度函数、质量函数。
P的参数特征:在累计分布函数的基础上提取关键特征,将P的不同凸显出来,其中最关键的特征是期望和方差以及在其之上衍生出来的矩的概念。
P的整体特征:从P的期望中衍生出的特殊的期望,也就是熵。
根据P的不同描述,衍生出三门学科:概率论、数理统计、信息论。
注:这里对学科的划分知识up主自己的看法,并不一定是权威的。尽信书则不如无书,要有自己的判断。
写在最后:
本篇文章从概率空间的三层结构说起,系统介绍了其中原理和各对应学科的联系。
但是在学习的过程中我愈发感觉自己知识的浅薄,似乎以前在学校课程的学习都只是为了考试,为了应对那些具体的题目,而考过之后就慢慢淡忘。我觉得这样的学习是无效的,特别是在数学方面的学习上。
所以我准备接续本系列,从头开始学习概率论、数理统计、信息论的相关知识,脱离考试的压力,多一些自己的思考,可以从整体上构建起这个框架并不断完善。(立一个flag)



