写在最前面：本篇文章时学习后的收获总结，学习流程大体如下：看视频—> 根据ppt整理 —> 阅读笔记后进行补充。（笔记自看，多思考；实践必做，跑dome)
我将使用深区域进行笔记的最后补充。（深区域就是这行字所在的区域）

人工智能三学派

什么是人工智能？让机器具备人的思维和意识。

三大学派

笔记补充

连接主义的神经网络

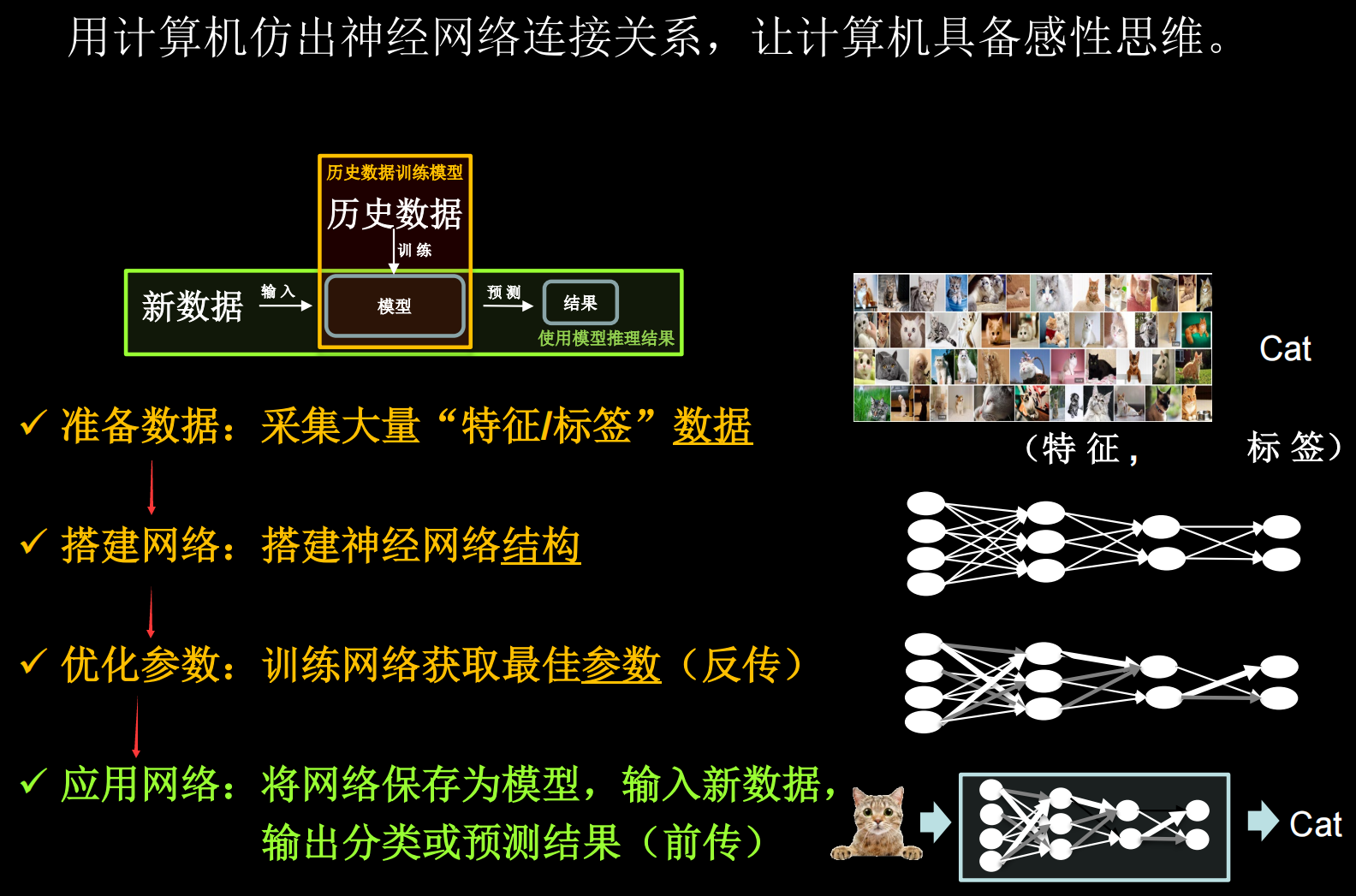
基于连接主义的神经网络模仿神经元，使计算机具有感性思维。图 1.2展示了从出生到成年，人脑中神经网络的变化。

随着我们的成长，大量的数据通过视觉、听觉涌入大脑，使我们的神经网络连接，也就是这些神经元连接线上的权重发生了变化，有些线上的权重增强了，有些线上的权重减弱了。如图 1.3 所示

基于连接主义的神经网络设计过程

神经网络设计过程?

我们要用计算机模仿刚刚说到的神经网络连接关系，让计算机具备感性思维。
首先，需要准备数据，数据量越大越好，要构成特征和标签对。如要识别猫，就要有大量猫的图片和这个图片是猫的标签，构成特征标签对。
随后，搭建神经网络的网络结构，并通过反向传播，优化连线的权重，直到模型的识别准确率达到要求，得到最优的连线权重，把这个模型保存起来。
最后，用保存的模型，输入从未见过的新数据，它会通过前向传播，输出概率值，概率值最大的一个，就是分类或预测的结果。下图展示了搭建与使用神经网络模型的流程。

神经网络设计过程

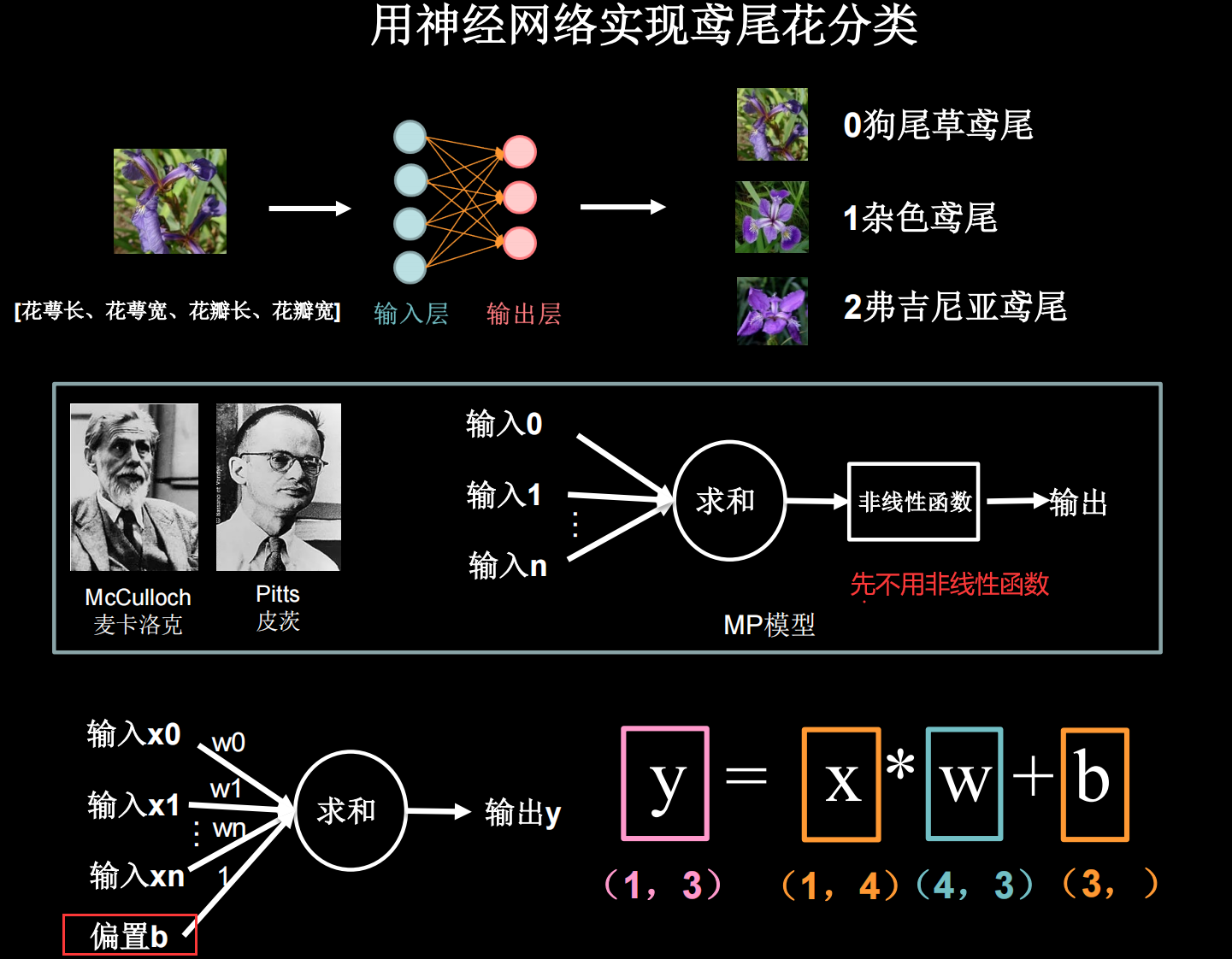
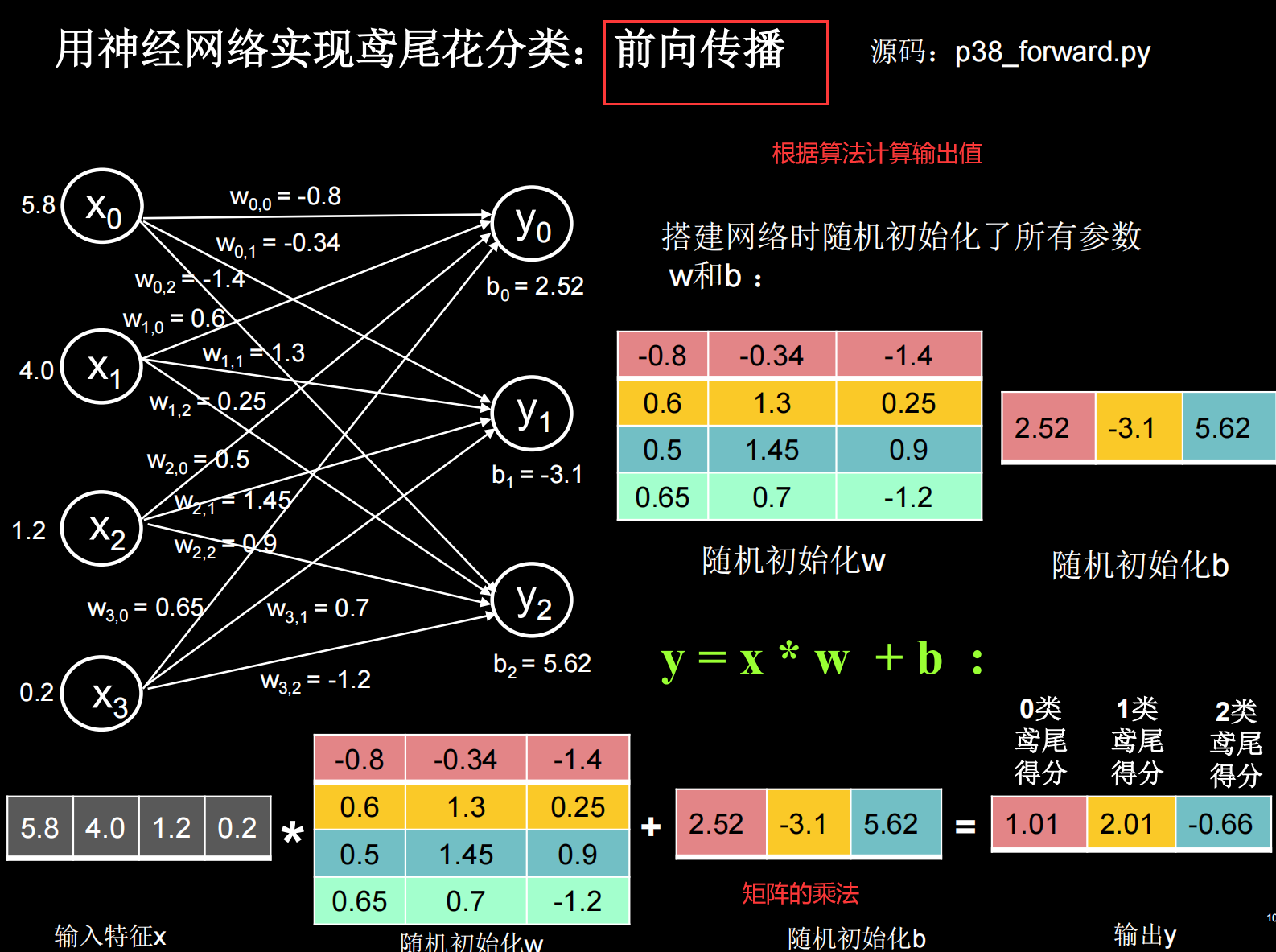
举一个例子：给鸢尾花分类（Iris）

eg1

eg2

搭建网络

喂入数据

前向传播

损失函数

梯度下降

反向传播

示例代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40

for epoch in range(epoch):  
# for epoch 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环40次迭代。
    with tf.GradientTape() as tape:  
	# with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  
	# .gradient函数告知谁对谁求导

    w.assign_sub(lr * grads)  
	# .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))

# lr初始值：0.2   请自改学习率  0.001  0.999 看收敛过程
# 最终目的：找到 loss 最小 即 w = -1 的最优参数w

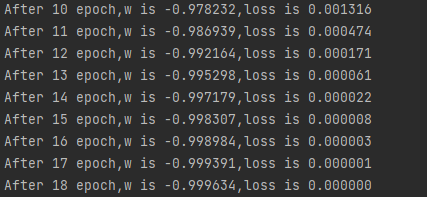
代码结果：
结果

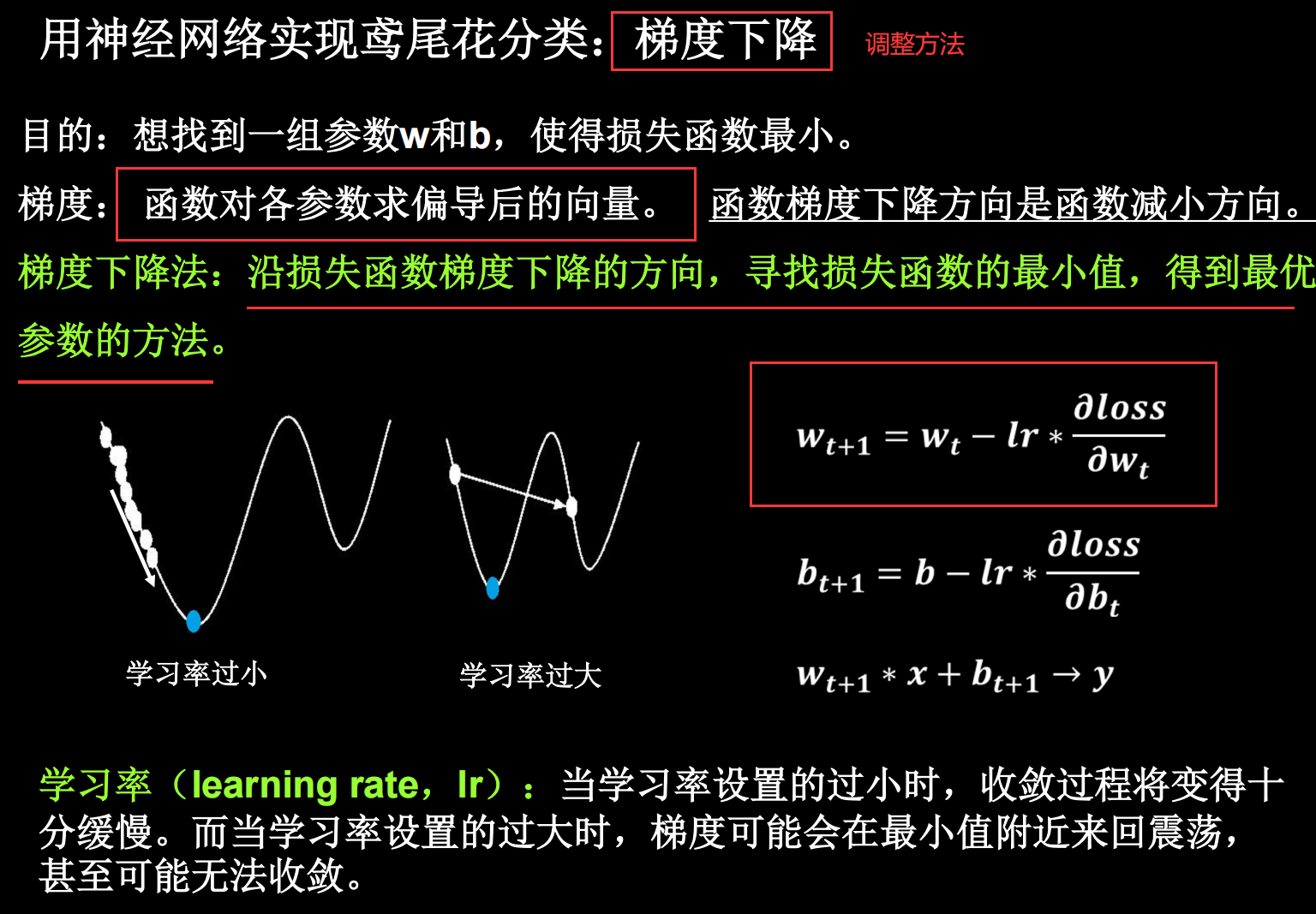
可见，经过18次迭代之后就可以得到最小值。但是如果学习率过小，经过40次迭代也无法得到最小值；如果学习率过大，会在最小值之间跳动，也无法得到最小值。所以我们需要通过更加科学的方法动态调整学习率，以达到最佳识别效果。

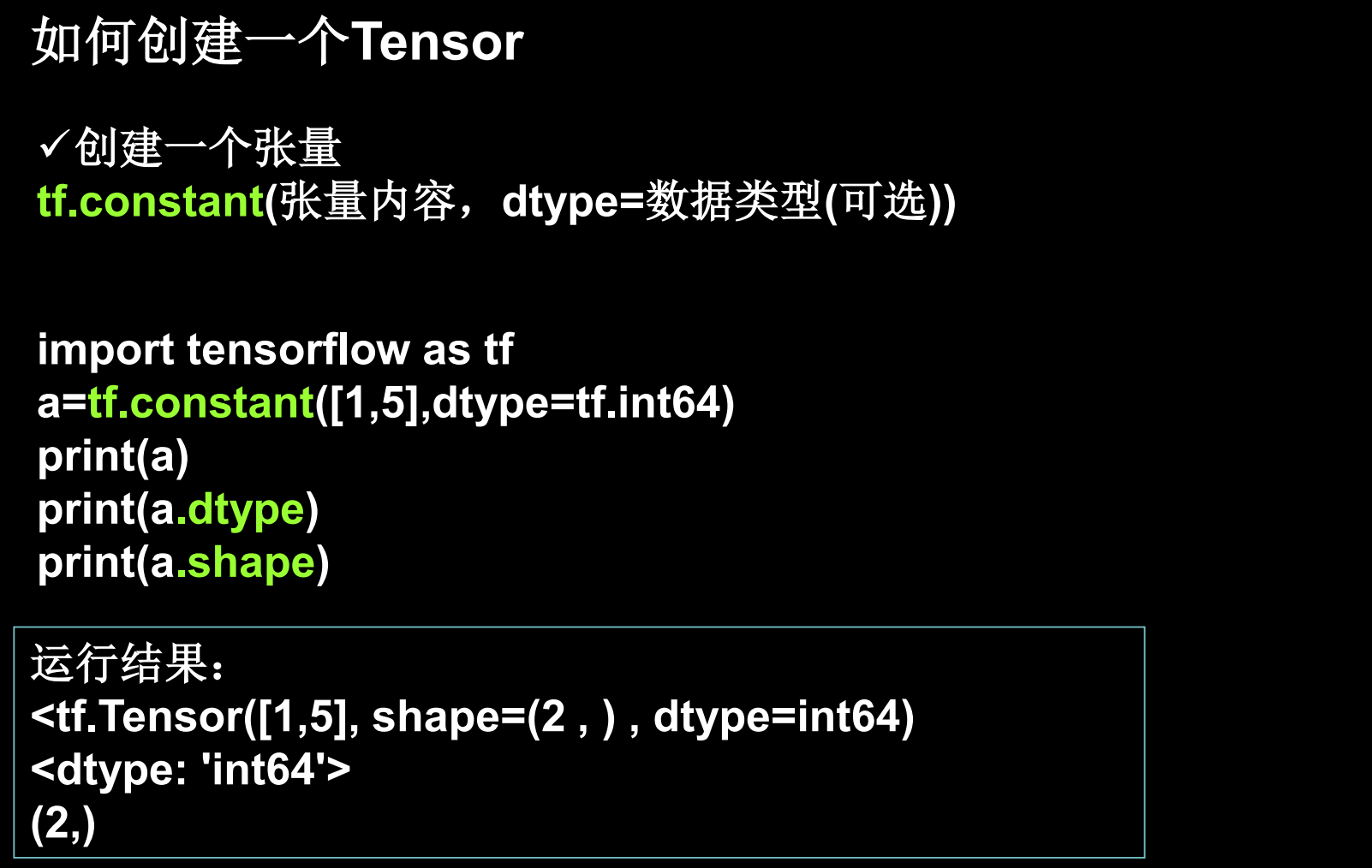
张量生成

张量是TensorFlow的基础，从其名称就可以看出来。属于tensorflow的数据类型。
关于张量的知识有很多，下面我们以其中的几个典型来介绍：

张量

dtype

创建一个张量

注：这里使用tf.constant创建的张量属于常量。要使用[xx]格式给出具体值，这里有几层中括号其维度就是多少，具体可以看上张量图。

np转换

注：将numpy生成的一维数组转换为张量（带有维度、数据类型）

同数张量

注：使用这种方法可以创建数据相同的张量。不过其参数要给出维度，逗号分隔开几个数就有几维。

正态分布

eg

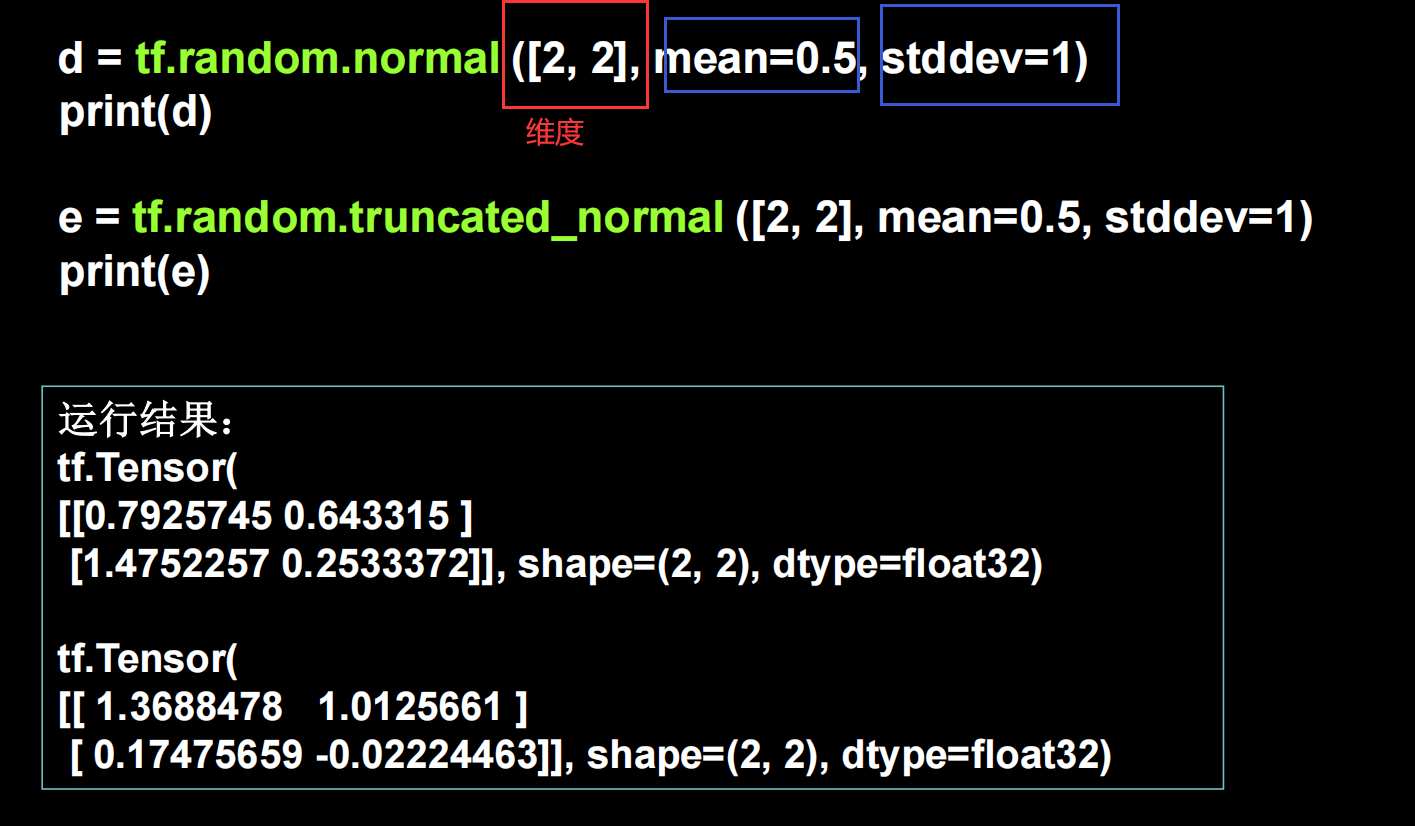
注：函数较长，但是都是属于random。并且这个是属于随机生成，不需要指定数据。

均匀分布

注：与上正态分布格式类似，不过分布不同。

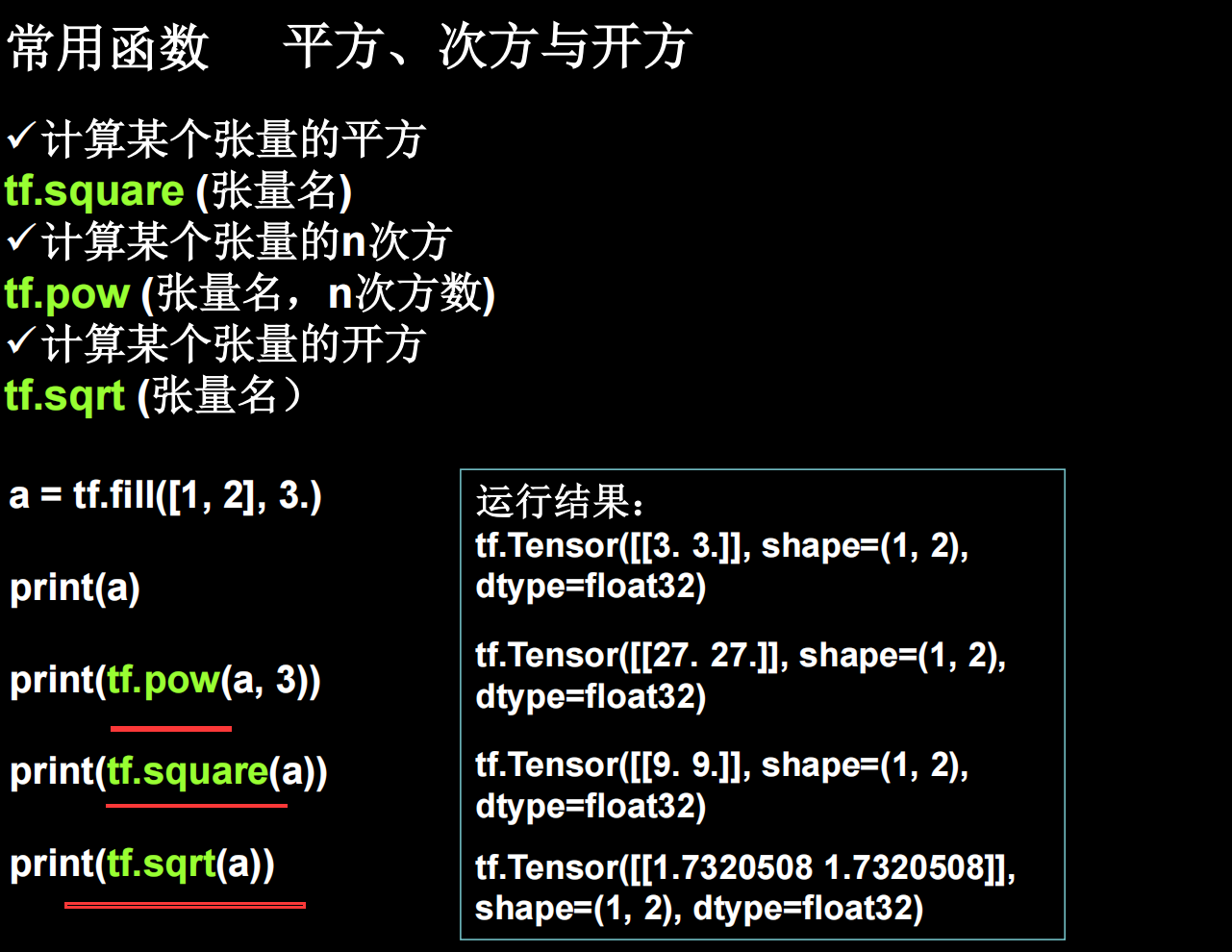
常用tf函数

tf.cast与tf.reduce_max+tf.reduce_min

常用函数1

注：使用cast转换后仍为张量，只是改名数据类型。
注2：tf.reduce有很多类别，上面已经有了max和min，取值后仍为张量。
代码示例：

1
2
3
4
5
6
7
8
import tensorflow as tf

x1 = tf.constant([1., 2., 3.], dtype=tf.float64)
print("x1:", x1)
x2 = tf.cast(x1, tf.int32)
print("x2", x2)
print("minimum of x2：", tf.reduce_min(x2))
print("maxmum of x2:", tf.reduce_max(x2))

axis

axis示例

注：这里的axis可以指定计算的区域，0为纵向，1为横向。

代码示例：

1
2
3
4
5
6
7
import tensorflow as tf

x = tf.constant([[1, 2, 3], [2, 2, 3]])
print("x:", x)
print("mean of x:", tf.reduce_mean(x))  # 求x中所有数的均值
print("sum of x:", tf.reduce_sum(x, axis=1))  # 求每一行的和

变量
注：使用tf.Variable可以生成变量，常用于训练量。

数学运算

四则运算

eg1

三方运算

矩阵乘法

注：矩阵乘法的计算过程要知道。

配对

eg

代码示例：

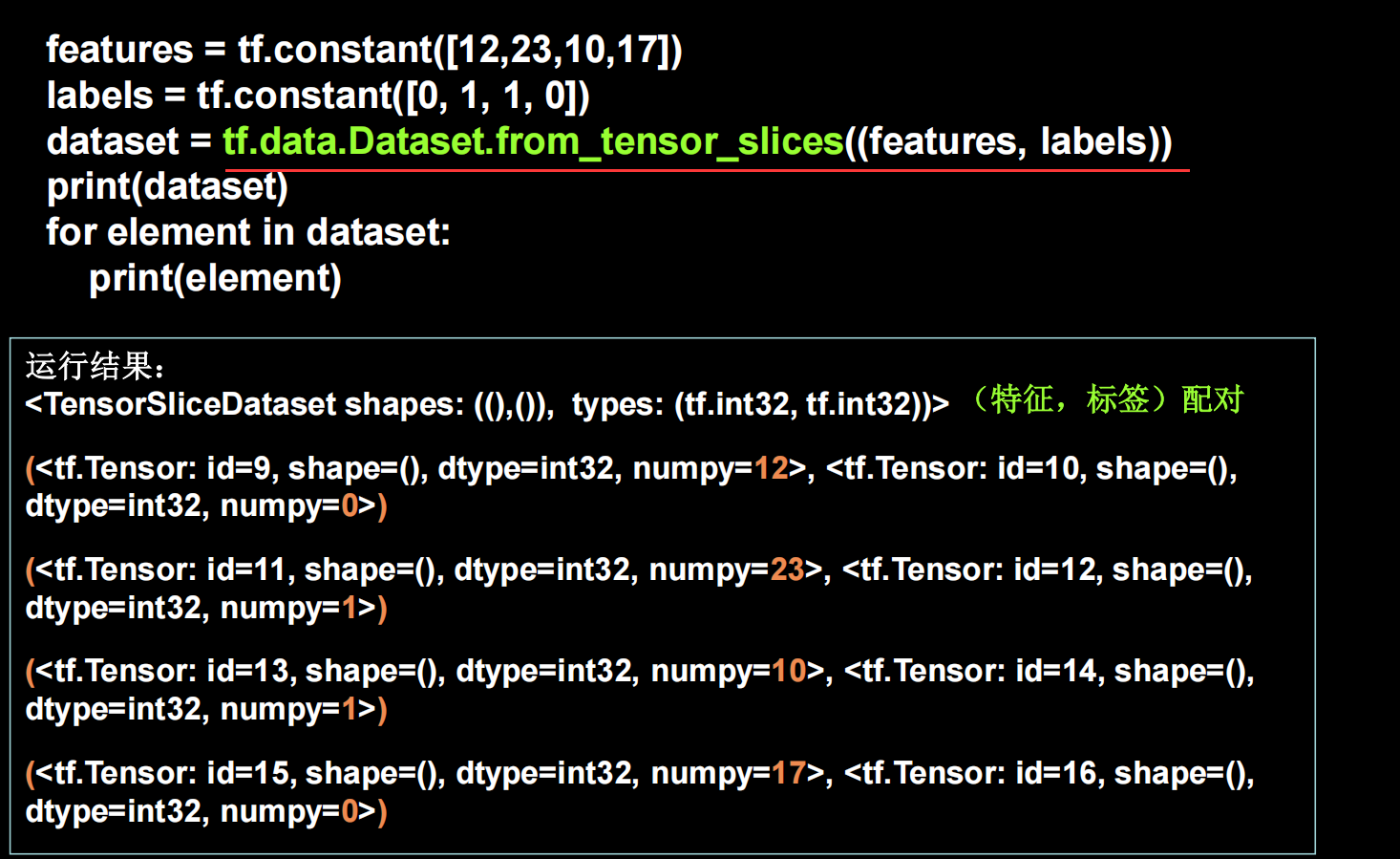
1
2
3
4
5
6
7
8
import tensorflow as tf

features = tf.constant([12, 23, 10, 17])
labels = tf.constant([0, 1, 1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
for element in dataset:
    print(element)

求导+with

索引

注：可利用 enumerate(列表名)函数枚举出每一个元素，并在元素前配上对应的索引号，常在 for 循环中使用。

one_hot

注：可用tf.one_hot(待转换数据，depth=几分类)函数实现用独热码表示标签，在分类问题中很常见。标记类别为为 1 和 0，其中 1 表示是，0 表示非。如在鸢尾花分类任务中，如果标签是 1，表示分类结果是 1 杂色鸢尾，其用把它用独热码表示就是 0,1,0，这样可以表示出每个分类的概率：也就是百分之 0 的可能是 0狗尾草鸢尾，百分百的可能是 1 杂色鸢尾，百分之 0 的可能是弗吉尼亚鸢尾。

eg

softmax
注：属于激活函数的一种，用于将输出的结果转换为符合的概率分布，用于与独热码匹配。

eg

自减

取下标

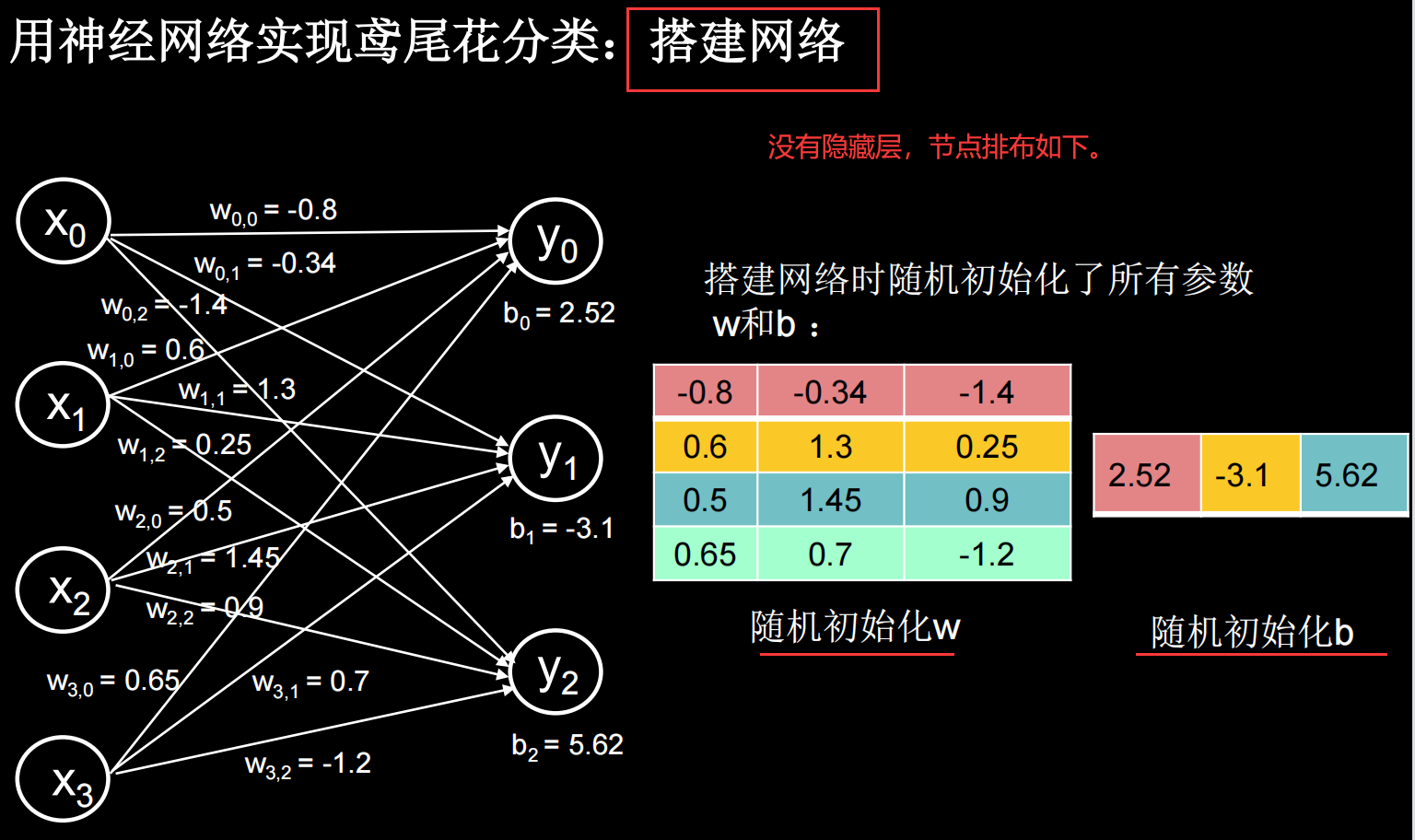
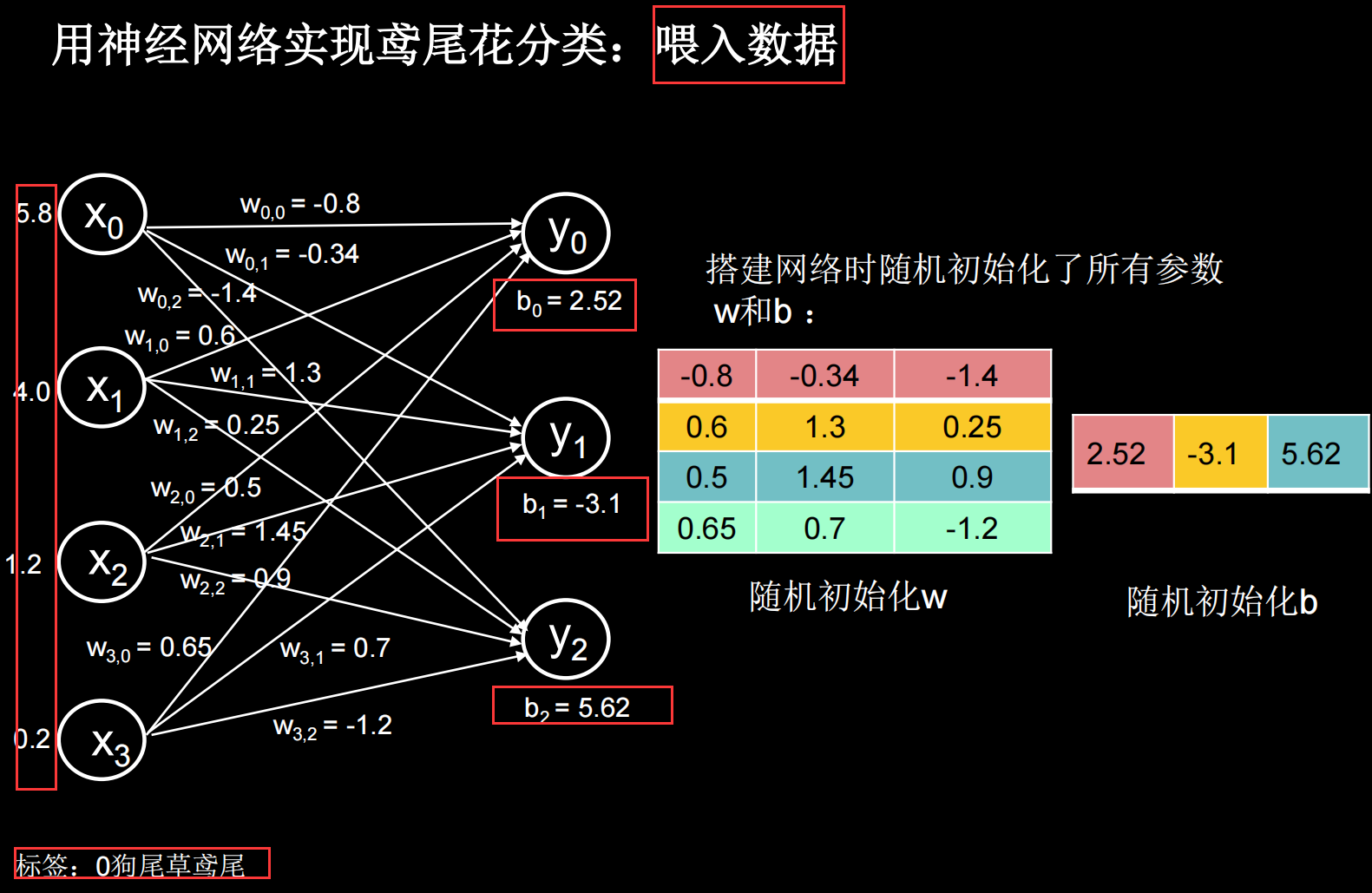
实例：神经网络实现鸢尾花分类（简化）

数据集

数据集导入
注：data的格式为150x4的矩阵，target的格式为150的数组。

结构

具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
# -*- coding: UTF-8 -*-
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np

# 导入数据，分别为输入特征和标签
# scikit-learn 内置有一些小型标准数据集，不需要从某个外部网站下载任何文件，用datasets.load_xx()加载。
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
print(x_data, y_data)

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

# 训练部分
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        # 实现梯度更新 w1 = w1 - lr * w1_grad    b = b - lr * b_grad
        w1.assign_sub(lr * grads[0])  # 参数w1自更新
        b1.assign_sub(lr * grads[1])  # 参数b自更新

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all/4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

对以上代码的补充分析：

1、数据集读入、数据集乱序、将数据集分割成永不相见的训练集和测试集、将数据配成[输入特征，标签]对。

补充1：
人类在认识这个世界的时候信息是没有规律的，杂乱无章的涌入大脑的，所以喂入神经网络的数据集也需要被打乱顺序。

补充2：
因为使用了同样的随机种子，所以打乱顺序后输入特征和标签仍然是一一对应的。

补充3：
使用 from_tensor_slices 把训练集的输入特征和标签配对打包，将每 32 组输入特征标签对打包为一个 batch，在喂入神经网络时会以 batch 为单位喂入。

训练过程？

补充1：
用两层 for 循环进行更新参数：第一层 for 循环是针对整个数据集进行循环，故用 epoch 表示；第二层 for 循环是针对 batch的，用 step 表示。

补充2：
因为训练集有 120 组数据，batch 是 32，每个 step 只能喂入 32 组数据，需要 batch 级别循环 4 次，所以 loss 除以 4，求得每次 step 迭代的平均 loss。

扩展方法

梯度爆炸?

参数更新量为学习率与损失函数偏导数相乘，二者乘积过大，则会导致梯度爆炸。
解决梯度爆炸问题可针对学习率进行调整，也可对数据进行调整。

故解决方法可为：
(1)逐步减小学习率，0.1、0.01 等；
(2)对数据进行预处理后再输入神经网络，减小偏差值的大小，抑制梯度爆炸，即数据归一化与标准化，其主要方法有线性归一化、非线性归一化、Z-Score 标准化。

以线性归一化为例，其代码实现如下：

1
2
3
4
5
6
7

def normalize(data):
	x_data = data.T # 每一列为同一属性，转置到每一行
	for i in range(4):
		x_data[i] = (x_data[i] - tf.reduce_min(x_data[i])) / 
		(tf.reduce_max(x_data[i]) - tf.reduce_min(x_data[i]))
 	return x_data.T # 转置回原格式

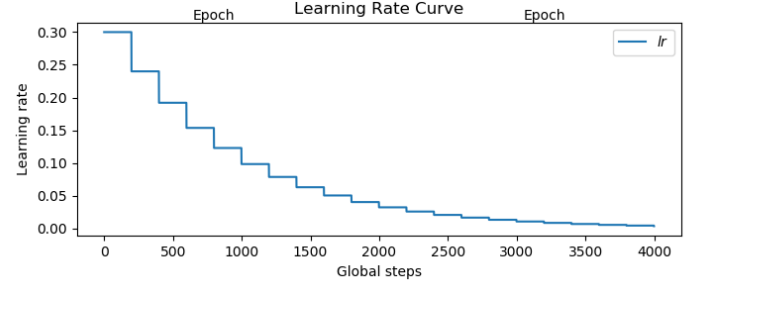
指数衰减学习率：指数衰减学习率可在训练初期赋予网络较大学习率，并在训练过程中逐步减小，可有效增加网络收敛速度。
在 tensorflow 中对应函数为
tf.compat.v1.train.exponential_decay(learning_rate_base,global_step,decay_step,deca y_rate,staircase =True(False),name)，当 staircase 为 True 时，学习率呈现阶梯状递减。

学习率